Hay muchas propiedades que nos permiten saber el valor de un determinante de una forma mucho más fácil que la que se ha visto hasta ahora. No solamente permiten simplificar el cálculo, si no que hacen posible que se pueda hallar determinantes de orden superior, para los que ya no hay una regla como en el caso de orden 2 y 3. Las comprobaciones de las mismas se pueden hacer fácilmente desarrollando los determinantes.
1) Si una matriz cuadrada tiene todos los elementos de una fila o columna nulos, su determinante es 0.


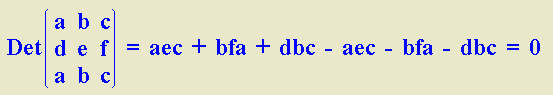






5) El determinante de una matriz A es igual al determinante de la transpuesta de A.





8) Si una fila de la matriz A se multiplica por un escalar k y se suma a otra fila de A, entonces el determinante de la matriz resultante es igual al determinante de A, det A. Lo mismo se cumple para las columnas de A. (Combinación lineal).


Multiplicando la segunda columna de A por el escalar 2 y sumándola a la columna 3 se obtiene la matriz B siguiente:

↓


9) Si A y B son matrices de , el determinante del producto AB es igual al producto de los determinantes de A y de B.
, el determinante del producto AB es igual al producto de los determinantes de A y de B.






1) Si una matriz cuadrada tiene todos los elementos de una fila o columna nulos, su determinante es 0.
Desarrollando por cofactores de la primera fila se tiene:


2) Si una matriz cuadrada tiene dos filas o dos columnas iguales su determinante es 0.
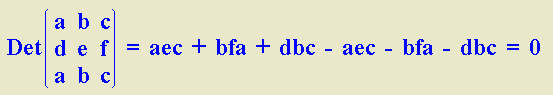
Ejemplo:

3) Si multiplicamos todos los elementos de una fila o columna de una matriz cuadrada por un número k, su determinante queda multiplicado por dicho número.
Multiplicando el tercer renglón de A por el escalar k = 3 se tiene la matriz B siguiente


4) Si una matriz cuadrada tiene dos filas o columnas proporcionales su determinante es 0. (Es una mezcla de las propiedades 2 y 3).
6) Si se intercambian dos filas o dos columnas de una matriz A entonces el determinante cambia de signo.
Ejemplo:

Intercambiando las filas 1 y 2 la matriz queda:

7) El valor de un determinante triangular es igual al producto de la diagonal principal
8) Si una fila de la matriz A se multiplica por un escalar k y se suma a otra fila de A, entonces el determinante de la matriz resultante es igual al determinante de A, det A. Lo mismo se cumple para las columnas de A. (Combinación lineal).

Multiplicando la segunda columna de A por el escalar 2 y sumándola a la columna 3 se obtiene la matriz B siguiente:

↓

Desarrollando por cofactores de la primera columna se tiene:
9) Si A y B son matrices de
El producto:
10) El determinante de la matriz identidad I es igual a 1 (uno)
11) Si todos los elementos de una fila o columna de una matriz cuadrada se descomponen en dos sumandos, entonces su determinante es igual a la suma de dos determinantes que tienen en dicha fila o columna el primero y el segundo sumando respectivamente, siendo los restantes elementos iguales a los del determinante inicial.
12) Si a una fila o columna de una matriz cuadrada se le suma otra paralela a ella multiplicada por un número, su determinante no varía.










0 comentarios :
Publicar un comentario