Método por definición




  •  El método e aconsejable para matrices 2x2 (no aconsejable para matrices de orden 3 o superior)
Paso para calcular la inversa
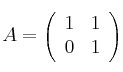
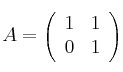
Supongamos que nos piden calcular la inversa de la matriz             A = \left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right)

  •  1) Asignamos a los elementos de la matriz inversa (que desconocemos) letras: a, b, c, ..
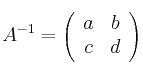
A^{-1} = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)

  •  2) Planteamos la igualdad de la definición: A \cdot A^{-1} = I 
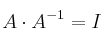
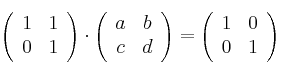
\left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right) \cdot \left( \begin{array}{cc} a & b \\ c & d \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)

  •  3) Resolvemos el producto de matrices A \cdot A^{-1} 
\left( \begin{array}{cc} a+c & b+d \\ c & d \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)

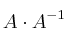
  •  4) Igualamos elemento a elemento
a+c=1
c=0
b+d=0
d=1

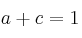
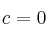
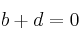
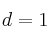
  •  5) Resolvemos los sistemas de ecuaciones resultantes
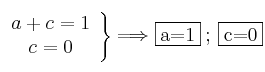
\left. \begin{array}{cc} a+c=1 \\c=0 \end{array} \right\} \Longrightarrow \fbox{a=1} \: ; \: \fbox{c=0}
\left. \begin{array}{cc} b+d=0 \\d=1 \end{array} \right\} \Longrightarrow \fbox{d=1} \: ; \: \fbox{b=-1}
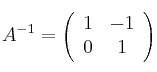
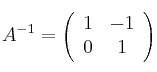
Por tanto la inversa es         A^{-1} = \left( \begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right)

0 comentarios :

Publicar un comentario